Introduction

Backtracking is a powerful algorithmic technique used in solving a wide range of problems, especially those that involve making a series of choices or decisions to reach a solution. In this blog, we will delve into the concept of backtracking and illustrate it with a classic problem known as the "Rat in a Maze."

What is Backtracking?

Backtracking is a systematic way of searching for solutions to problems by exploring all possible options and undoing them when they lead to a dead end. This technique is often used in optimization, puzzle-solving, and decision-making scenarios. The idea is to try various paths, backtrack when necessary, and continue the search until a valid solution is found or all possibilities are exhausted.

The Rat in a Maze Problem

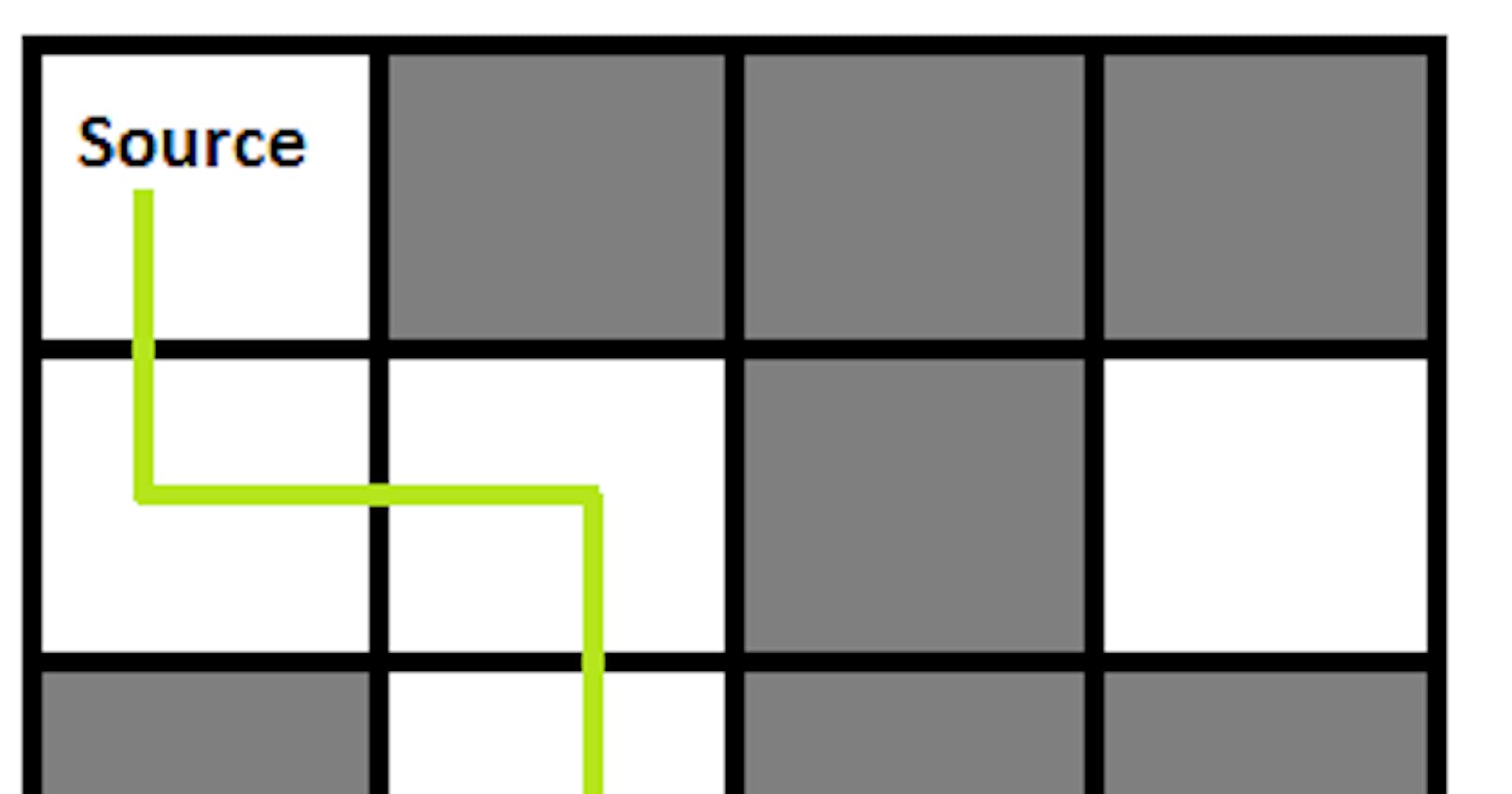
The Rat in a Maze problem is a classic illustration of the backtracking technique. In this problem, we are presented with a maze, usually represented as a grid, where a rat starts at a specific position and must find its way to the exit while avoiding obstacles. The objective is to find a path from the starting point to the exit, if it exists.

Key elements of the problem:

1. A maze grid.

2. A starting position for the rat.

3. An exit position.

4. Obstacles or blocked paths.

The goal is to determine whether there is a valid path from the starting point to the exit point and find that path if it exists.

Backtracking in Action: Solving the Rat in a Maze Problem

Let's break down the steps to solve the Rat in a Maze problem using backtracking:

1. Create a grid to represent the maze. Each cell can be empty (indicating a valid path), blocked (indicating an obstacle), or visited (to track the path taken by the rat).

2. Define a recursive function to explore the maze. This function should take the current position of the rat as an argument.

3. Within the function, check if the current position is outside the maze boundaries or is blocked. If any of these conditions are met, return false to indicate that this path is invalid.

4. If the current position is the exit point, return true to indicate that a valid path has been found.

5. Within the recursive function, try moving the rat in all possible directions (up, down, left, and right) one step at a time. For each move, make a recursive call to explore the next position.

6. If any of the recursive calls return true, it means a valid path has been found, and the current position is part of that path. Mark the current position as visited and return true.

7. If none of the recursive calls result in a valid path, mark the current position as visited and return false to backtrack and explore other possibilities.

8. Continue this process until the rat either reaches the exit point, and a valid path is found, or all possible paths have been explored.

Here is a simple C++ implementation of the Rat in a Maze problem using backtracking:

#include <iostream>
#include <vector>

using namespace std;

// Define the size of the maze
const int N = 5; // You can change this to match the size of your maze

// Function to print the solution path
void printSolution(vector<vector<int>>& sol) {
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < N; j++) {
            cout << sol[i][j] << " ";
        }
        cout << endl;
    }
}

// Function to check if a given cell is a valid move
bool isSafe(vector<vector<int>>& maze, int x, int y) {
    return (x >= 0 && x < N && y >= 0 && y < N && maze[x][y] == 1);
}

// Recursive function to solve the Rat in a Maze problem
bool solveMazeUtil(vector<vector<int>>& maze, int x, int y, vector<vector<int>>& sol) {
    if (x == N - 1 && y == N - 1) {
        sol[x][y] = 1; // Reached the exit
        return true;
    }

    if (isSafe(maze, x, y)) {
        sol[x][y] = 1; // Mark the current cell as part of the path

        // Move forward in both the x and y directions
        if (solveMazeUtil(maze, x + 1, y, sol) || solveMazeUtil(maze, x, y + 1, sol)) {
            return true;
        }

        // If moving in both directions doesn't lead to a solution, backtrack
        sol[x][y] = 0;
        return false;
    }

    return false;
}

// Function to solve the Rat in a Maze problem
bool solveMaze(vector<vector<int>>& maze) {
    vector<vector<int>> sol(N, vector<int>(N, 0)); // Initialize the solution matrix

    if (!solveMazeUtil(maze, 0, 0, sol)) {
        cout << "No solution exists." << endl;
        return false;
    }

    cout << "Solution:" << endl;
    printSolution(sol);
    return true;
}

int main() {
    vector<vector<int>> maze = {
        {1, 0, 0, 0, 0},
        {1, 1, 0, 1, 0},
        {0, 1, 0, 0, 0},
        {0, 1, 1, 1, 1},
        {0, 0, 0, 0, 1}
    };

    solveMaze(maze);

    return 0;
}

Conclusion

Backtracking is a valuable technique for solving problems with multiple decision points, where exploring all possible solutions is necessary. The Rat in a Maze problem is a classic example that demonstrates the power of backtracking in finding a path through a complex maze. By systematically exploring the maze while keeping track of visited cells, we can determine if a solution exists and, if so, discover the path to success. Backtracking is a versatile tool that can be applied to various other problems, making it a fundamental skill in the world of algorithmic problem-solving.